从二维点集重建平面形状的思考：GHPython实现

前言：从村落平面问题到二维点集重建

​ 意识到这个问题并不是简单的凸包，要从昨天晚上麦同学给出的一个几何问题提起：

图1 在这样的平面图中，我需要通过精确可控的方式将该村落的建筑实体轮廓通过多段直线（ployline）包裹起来，以达成从宏观视角审视聚落形态的目的

Q：一个村落，如何通过设定一定的阈值，使其生成不同内凹程度的边界包裹？

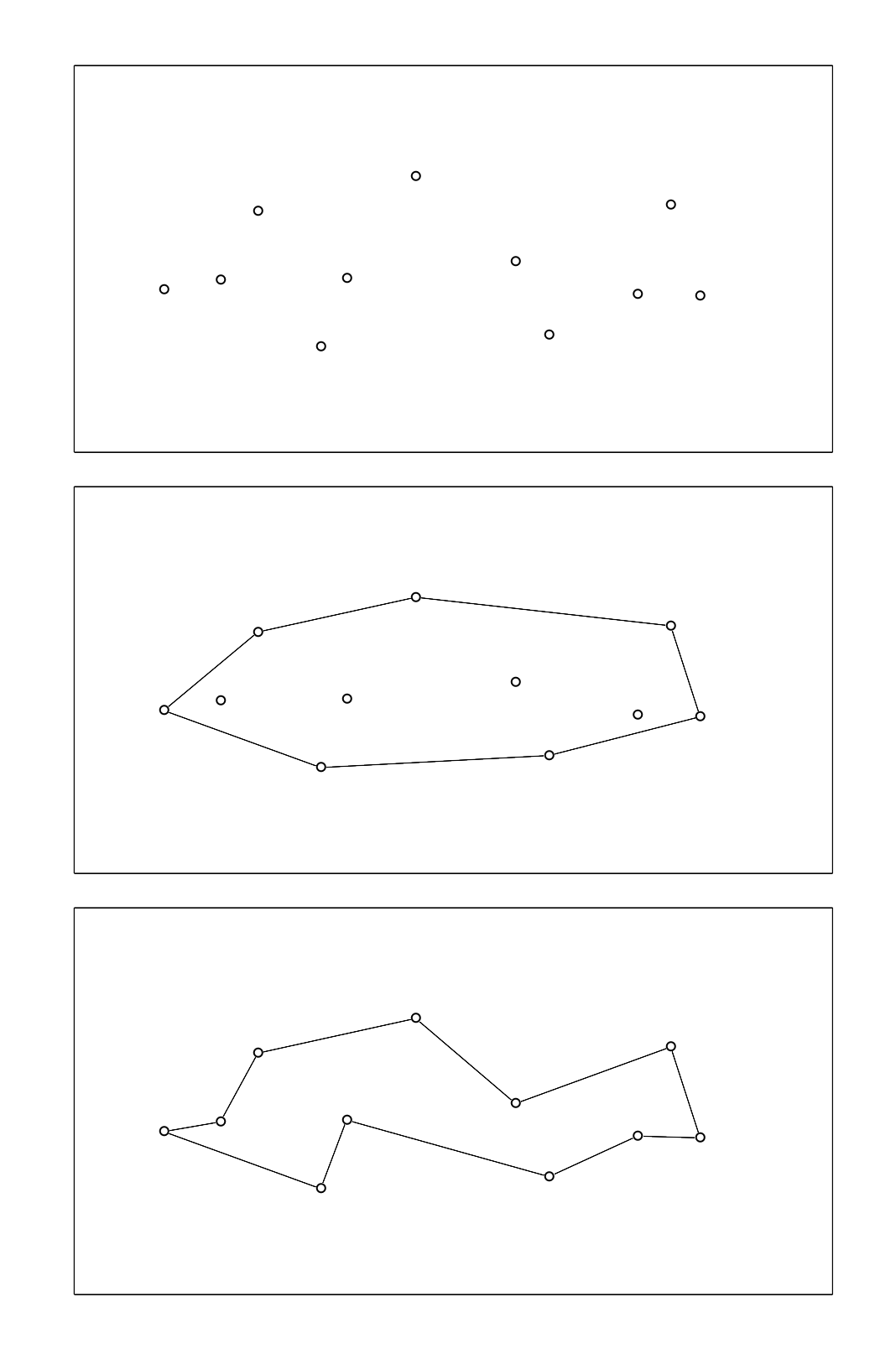
​ 当我们有一系列点的时候，如何从点集中重建一个合理的集合形状？这个问题在三维点集中存在，但是本问题主要聚焦于平面，将其转化一下，可以将问题变为：

给出平面区域的一系列散点，要求出一定程度上反应这些散点的平面多边形，给出边的连接方式即可。

图2 凸包处理和预期效果之间的区别

​ 从示意图中可以看到，相较于简单粗暴的「凸包算法」，后者并不局限于出现「内凹」的情况，因此在精准描述轮廓的情况下有更强的适用性。

​ 查阅资料后意识到，诸如此类问题往往存在两种主要类型:

​ 给出的点集是表征图形边界的

​ 给出的点集表征图形的覆盖范围的

​ 这两种不同的含义是和具体的应用场景相关的。

求散点描绘的轮廓	求散点分布区域的边界轮廓

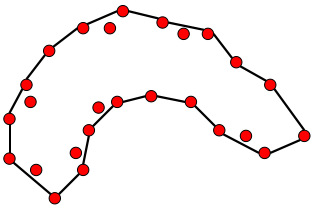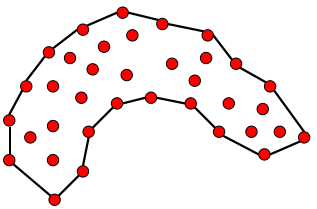凹包与Alpha Shape

​ 当前已经有不少集合领域的资料探讨过这类问题的解决方案，但是篇幅有限，此处仅按网友chnhideyoshi提供的思路发散，在GHPython中进行复现。

​ 首先，很多之前了解过算法的人都知道凸包算法，凸包求解的是覆盖所有点的凸多边形，由于限定死了凸多边形，所以凸包显然不是本文想要讨论问题的解决方案。我希望找到的解法不能否定凹陷的部分，因此可以联想到这个问题是否可以被定义为「凹包」。或者说一种广义的参数化的凸包。事实上确实有凹包的概念，英文叫做concave hull（与之对应，凹包被叫做convex hull）。不过由于凸包的情况不同，凹包没有特别明确的定义，给定一个较不规则的点集，可以有各种各样的凹包，但是凸包是唯一确定的。

图3 Grasshopper中自带的求解凸包模块

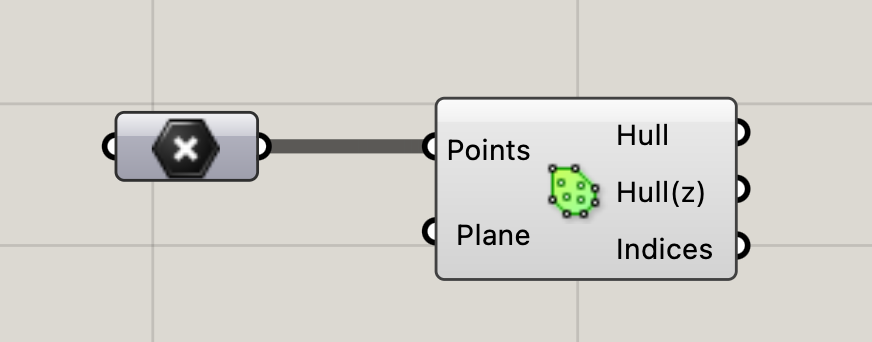
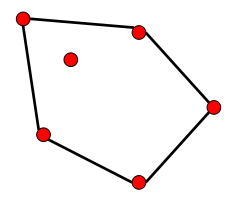
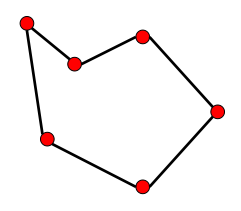
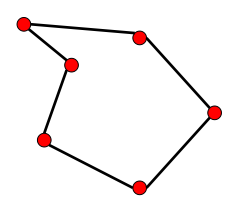
凸包	凹包A	凹包B

​ 在论文中提到了名为alpha shape的概念，简单解释来说，alpha shape其实就是在凸包的基础上多了一个可以设定的参数α，因为这个α，在alpha shape进行形状重建的过程中可能就不会像凸包一样连接相距较远的顶点。参数α若趋于无穷大，那么这个图形就会无限接近凸包；而α取小了，alpha shape就会倾向于在一定位置凹陷进去，以更加贴合点集的外形。选择合理的α就能够控制生成的形状，让其更加符合点集所描绘的形状。

实现方法

基于Delaunay三角化

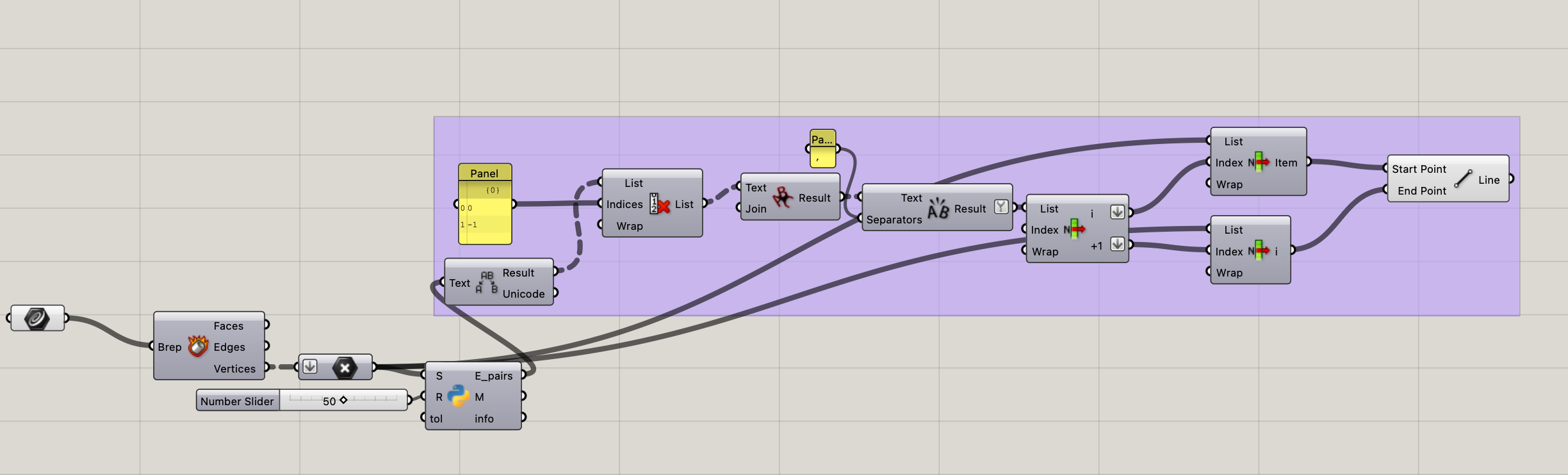
​ 经常使用grasshopper处理数据的话，一定会熟悉Delaunay来处理点之间的关系问题，例如，我们想要为目标点集使用Delaunay三角化算法，可以得到如下的三角网。

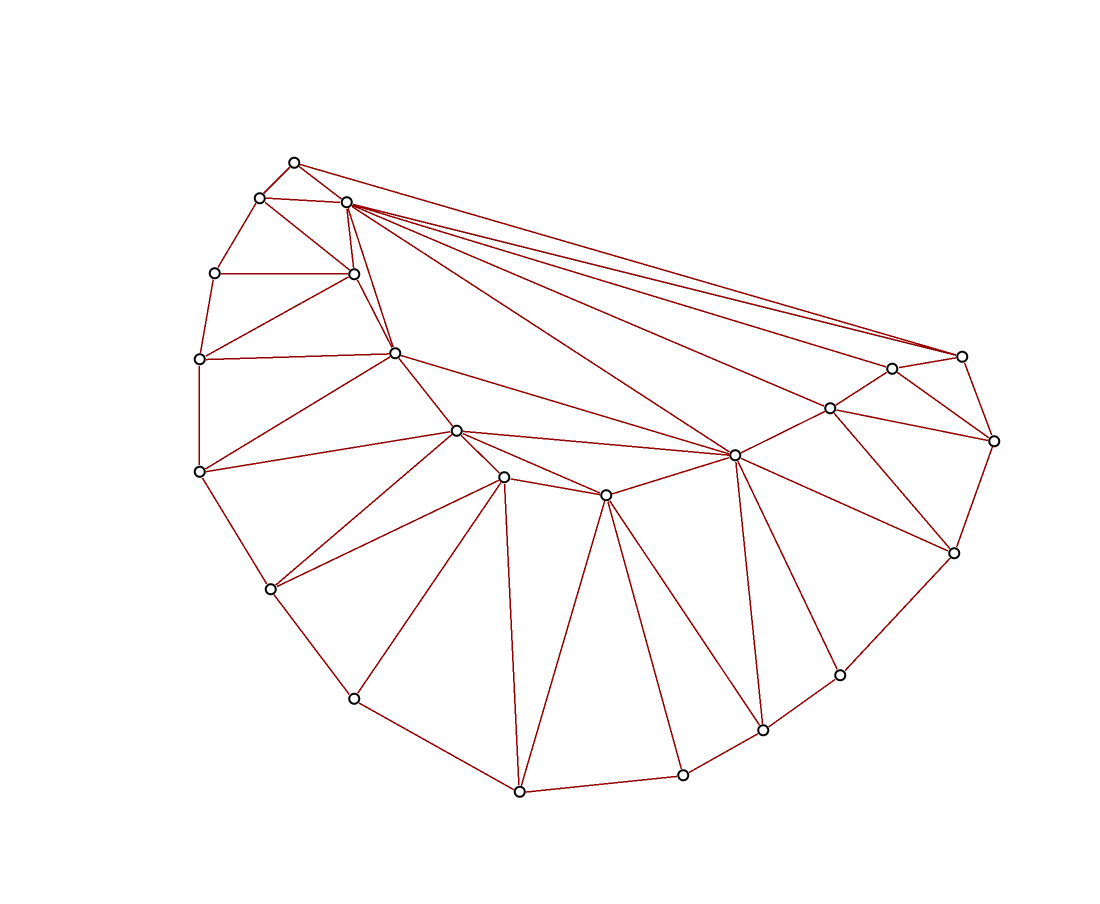
​ 分析得到的三角网，不难想到一个解决方法：因为我们想要求解的形状就是Delaunay三角网的子集，所以我们只需要从所以我们只需要从Delaunay三角网的最外层边开始外不断的删去超过长度限制的边，当这个过程结束时，我们就能够得到一个大致符合我们预期的形状。

​ 所以总结这个思路，输入点集S和长度限制R的求取凹包的列表算法过程如下：

1、为点集S求取Delaunay三角网M，三角网用标准的Mesh形式表示。

2、为M初始化所有的Edge对象，并求取Edge的长度以及邻接三角形集合。其中邻接三角形的边为内部边，1个三角形的为边界边，0个三角形的为计算过程中会退化的边。

3、将所有长度大于R的边界边加入队列，并当队列非空时循环下列过程：

​ i. 从队列中取出一条边E，得到E的唯一邻接三角形T。

​ ii. 找到T中另外两个边E1，E2，将它们的邻接三角形集合删去T。

​ iii. 将E1，E2中新形成的长度大于R的边界加入队列。

​ iv. 将E置无效标记，若E1，E2有退化的，也置无效标记。

4、收集所有有效的边界边，形成边列表，输出。

图4 Delaunay减边的具体方法

### 滚边法（Edge Pivoting）

​ 这是昨天晚上第一眼看到这个问题时想到的解法，但是实际在角度判断的过程中出现了很多的问题，所以后续查资料才找到实际的解决方案。

​ 这个方案从求凸包的Graham Scan算法衍生出来的一个方法。Graham Scan算法首先找到一个Y的最低点作为起始点，然后使用叉积角度判断的方法判断点的走向，最走在栈内留下凸包的点序列。具体的算法网上有不少现成的资料，在这里就不过多赘述了。而这个方法也是和Graham法从同一个出发点出发，通过扫描角度来确定下一个点。

图5 本动图描述了具体的实现逻辑

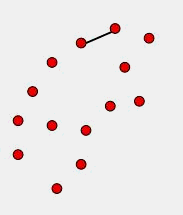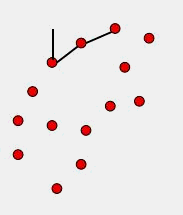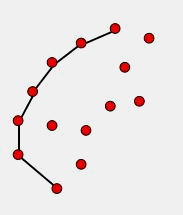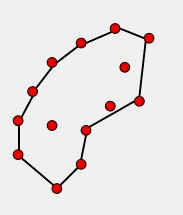
​ 首先要实现这个算法，需要对随机的点查询距离以及其几何距离在R内的所有点，即求所谓的R邻域。R邻域算法是KNN（K-nearest neighbors）算法的一个变形，可以在小于O(n²)的复杂度下求解R邻域。但是为了简单起见，本次复现因为场景点数目不大，所以使用的方法并没有过多考虑效率，实现R邻域的方式是先建立一个 n x n 的二维数组存储所有点两两之间的距离，然后遍历一次二维数组，为所有的点建立一个R邻域列表，该列表中存储了对应点R邻域的索引值，这个列表很有用，下面要介绍的滚球法也利用了这个列表。

​ 实际上不难理解，假设AB为凹包的一个边，那么其下一个点C必然是在B的R邻域点中选择。我们实现这个算法的关键，就是为AB边找一个合适的C点。这里笔者设想的寻找C的方法使用如下原则：

1. 假如B的R领域除了A就只有一个点，那么那个点就是C。
2. 以B为圆心从向量BA出发转圈扫描，遇到的第一个点为C。

　　这里涉及到一个小算法，即所谓的极坐标方向排序问题，这个问题的描述是：给定一个原点P和一个初始方向n，如何为平面上的点集S排序，使得点集中的点P1,P2…PN与P的连接是按从n开始的逆时针排列的。

​ 这个问题搜一搜stackoverflow即得到一个很好的解答，在该帖子里答主给出一个用于比较的函数，一旦有了比较函数，排序也不成问题，这个比较函数在后面的方法中会出现。其具体的比较原理如果对向量的点积叉积有所了解也不难理解。这里不妨提一下点集叉积的结果符号的几何含义：

1. 向量a与b的点集结果为一个实数，计算方式是ax * bx + ay * by，满足交换率，为正值代表ab夹角小于90度,为锐角，负值代表夹角大于90度（谈夹角的话是指0-180度范围），为钝角。
2. 向量a与b的叉积结果为一个向量，其数值的计算方法是ax * bx − ay * by，不满足交换率，为正值代表向量b处于向量a的逆时针方向（即a逆时针转一个小于180的角能转到b），负值代表向量b处于向量a的顺时针方向（即a顺时针转一个小于180的角能转到b，非要逆时针转则必然超过180度）。

　　那么找C点的第二条实现的方式就类似于对一个数组找最小值那样，通过比较找到最小的角度，这个有最小角偏向的就是C点。不过遗憾的是这个思路其实是问题的，测试表明对一些点集采用这个方法会有BUG出现。例如当C点出现在BA向量小于90度的方向时，形成的BC边和AB边具有大致相反的方向，会导致下一步的寻点出现逆向，故这个思路不算是一个成功的思路，不过失败是成功之母，它却引出另一个滚球法的思路，相比这个思路具有更好的鲁棒性。

滚球法（Ball Pivoting）

​ 对于任何点集，我们把这些点想象为钉在平面上的钉子。假如拿一个半径大于一定值的球去从边界接近这个钉群，我们可以用这个球在这些钉子群的边界滚一圈，每次滚动，球都能接触到两个钉子而被卡住。

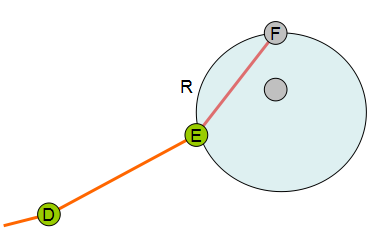
　　这个思路要求一个合法的R，R太小就没法形成一个闭合的图形。由于我们讨论问题的初衷是要形成一个合适的多边形而不是0个或多个，这样对R的选择就应该有一个限制，太小的R必然出不了结果，这里姑且假设给的R值是合适的。此过程若形成一个多边形，则多变形的最长的边一定小于球的直径。所以算法输入参数为R，意味着拿一个半径为R/2的圆去滚。如下图显示了这个滚球的过程：

图6 滚球法图解

​ 我们不难发现一个性质，即对于任何一次翻滚，假设从弦DE翻转到新弦EF，圆不可能扫过任何的其他点，因为假如扫到其他点，必然会被这个点所卡住，那么新弦就不可能是EF了。这样我们只需对极坐标排序后的E点的R邻域依次寻找符合不覆盖其他点的圆即可。

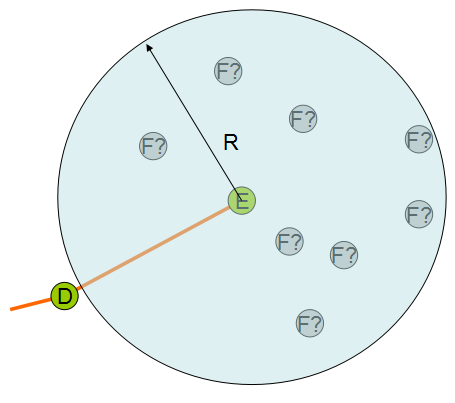
圆在翻滚的时候不能扫到其他点	对E的邻域测试圆覆盖情况寻找合适的F

​ 这个算法的执行过程和滚边法相似，算法结构都是先找起点，然后循环找下一个点，核心问题也是从DE线段出发寻找新线段EF，而不是再用边去扫描，而是用圆去扫描。分析后归纳出算法的大致步骤：

1、先求凸包那样求出一个Y值最小(Y值相同则取X最大)的点，作为初始点A，此点一定在凹包上。

2、从该点出发，(1,0)作为基准向量，先找一个小于R的边作为初始边，这时这个点即为B，此时一个半径为R/2的圆就卡在了AB上，此时第一个弦AB就找到了。

3、循环后寻找接下来的弦，假设上一条弦位DE，那么下一条弦必然从E开始，连接到E的一个R领域内的点F。寻找F可以使用如下的原则：先对E的R领域的点，以E为中心ED向量为基准进行极坐标方向排序，之后依次为R领域点F₀ → F_N建立以EF_i为弦的圆，然后检查其中是否包含其他F₀ → F_N的点，若不存在，则EF_i即为新弦，则跳出循环。

4、依次找到所有的弦，直到找不到新的弦或遇到以前已经作为弦的点为止。

​ 在R取值合适的情况下，这个过程一定能够给出一个闭合的图形。

## 附录：实际代码

### Delaunay减边法

>import math
>from collections import deque

>import Rhino
>import Rhino.Geometry as rg

>try:
>import ghpythonlib.components as ghcomp
>except ImportError:
>ghcomp = None


>def xy_key(pt, tol=1e-6):
>"""基于 XY 的 hash key，用于去重和索引映射。"""
>if tol <= 0: tol = 1e-6
>s = 1.0 / tol
>return (int(round(pt.X * s)), int(round(pt.Y * s)))

>def dist_xy(pa, pb):
>"""XY 距离"""
>return math.hypot(pa.X - pb.X, pa.Y - pb.Y)

>def mesh_face_triangles(msh):
>"""将 Mesh 面统一为三角集合，返回列表 [(a,b,c), ...]（顶点索引）"""
>tris = []
>fcol = msh.Faces
>for i in range(fcol.Count):
   f = fcol[i]
   if f.IsTriangle:
       tris.append((f.A, f.B, f.C))
   else:
       # Quad -> 两个三角
       tris.append((f.A, f.B, f.C))
       tris.append((f.A, f.C, f.D))
>return tris


>class EdgeInfo(object):
>__slots__ = ('i', 'j', 'adj', 'length', 'valid')
>def __init__(self, i, j, length):
   if i < j:
       self.i, self.j = i, j
   else:
       self.i, self.j = j, i
   self.adj = []    
   self.length = length
   self.valid = True
>def key(self):
   return (self.i, self.j)
>def etype(self):
   return len(self.adj)
>def invalidate(self):
   self.valid = False
   self.adj = []

>class TriInfo(object):
>__slots__ = ('vi', 'valid')
>def __init__(self, a, b, c):
   self.vi = (a, b, c)
   self.valid = True


>def build_delaunay_mesh(points):
>if ghcomp is None:
   raise RuntimeError("ghpythonlib.components 不可用。")
>res = ghcomp.DelaunayMesh(points)
>msh = res.mesh if hasattr(res, 'mesh') else res
>if msh is None or not isinstance(msh, rg.Mesh):
   raise RuntimeError("DelaunayMesh 生成失败。")
>msh.Normals.ComputeNormals()
>msh.Compact()
>return msh



>def concave_hull_edges_by_threshold(S, R, tol=1e-6):
>if not S or len(S) < 3:
   return [], [], None, {"error": "点数量不足"}

>key_to_orig = {}
>unique_pts = []
>for idx, p in enumerate(S):
   k = xy_key(p, tol)
   if k not in key_to_orig:
       key_to_orig[k] = idx
       unique_pts.append(p)
>if len(unique_pts) < 3:
   return [], [], None, {"error": "去重后点数量不足"}

>M = build_delaunay_mesh(unique_pts)

>vidx_to_orig = {}
>mv = M.Vertices
>for vi in range(mv.Count):
   p3f = mv[vi]
   p = rg.Point3d(p3f.X, p3f.Y, p3f.Z)
   k = xy_key(p, tol)
   oi = key_to_orig.get(k, None)
   if oi is None:
       best_i, best_d = -1, 1e100
       for j, sp in enumerate(S):
           d = (sp.X - p.X) ** 2 + (sp.Y - p.Y) ** 2
           if d < best_d:
               best_d = d
               best_i = j
       oi = best_i
   vidx_to_orig[vi] = oi

>tris_idx = mesh_face_triangles(M)  # [(a,b,c), ...]
>triangles = [TriInfo(a, b, c) for (a, b, c) in tris_idx]

>edges = {}  # (i,j) -> EdgeInfo
>def add_edge(a, b, tri_index):
   i, j = (a, b) if a < b else (b, a)
   key = (i, j)
   if key not in edges:
       pa = M.Vertices[i]; pb = M.Vertices[j]
       la = rg.Point3d(pa.X, pa.Y, pa.Z)
       lb = rg.Point3d(pb.X, pb.Y, pb.Z)
       length = dist_xy(la, lb)
       edges[key] = EdgeInfo(i, j, length)
   edges[key].adj.append(tri_index)

>for ti, (a, b, c) in enumerate(tris_idx):
   add_edge(a, b, ti)
   add_edge(b, c, ti)
   add_edge(a, c, ti)

>Q = deque()
>for key, e in edges.items():
   if e.valid and e.etype() == 1 and e.length > R:
       Q.append(key)

>while Q:
   key = Q.popleft()
   e = edges.get(key, None)
   if e is None or not e.valid:
       continue
   if e.etype() != 1:
       continue

   t_idx = e.adj[0]
   if t_idx < 0 or t_idx >= len(triangles):
       e.invalidate()
       continue
   T = triangles[t_idx]
   if not T.valid:

       continue

   a, b, c = T.vi

   tri_edges = {tuple(sorted((a, b))), tuple(sorted((b, c))), tuple(sorted((a, c)))}
   other_keys = [ek for ek in tri_edges if ek != key]

   for ek in tri_edges:
       ee = edges.get(ek, None)
       if ee is None or not ee.valid:
           continue
       if t_idx in ee.adj:
           ee.adj.remove(t_idx)

   if e.etype() == 0:
       e.invalidate()
   else:
       e.invalidate()

   T.valid = False

   for ok in other_keys:
       oe = edges.get(ok, None)
       if oe is None or not oe.valid:
           continue
       et = oe.etype()
       if et == 0:
           oe.invalidate()
       elif et == 1 and oe.length > R:
           Q.append(ok)

>boundary_edges = []
>for key, e in edges.items():
   if e.valid and e.etype() == 1:
       boundary_edges.append(e)

>E_lines = []
>E_pairs = []
>for e in boundary_edges:
   vi, vj = e.i, e.j
   pa = M.Vertices[vi]; pb = M.Vertices[vj]
   a3 = rg.Point3d(pa.X, pa.Y, pa.Z)
   b3 = rg.Point3d(pb.X, pb.Y, pb.Z)
   E_lines.append(rg.Line(a3, b3))
   oi = vidx_to_orig[vi]
   oj = vidx_to_orig[vj]
   if oi > oj:
       oi, oj = oj, oi
   E_pairs.append((oi, oj))

>stats = {
   "input_points": len(S),
   "unique_points": len(unique_pts),
   "mesh_vertices": M.Vertices.Count,
   "mesh_faces": M.Faces.Count,
   "triangles_count": len(triangles),
   "edges_total": len(edges),
   "boundary_edges_out": len(boundary_edges),
   "R": R
>}
>return E_lines, E_pairs, M, stats



>if 'tol' not in globals() or tol is None:
>tol = 1e-6

>try:
>E_lines, E_pairs, M, stats = concave_hull_edges_by_threshold(S, R, tol)
>info = " | ".join(f"{k}: {v}" for k, v in stats.items())
>except Exception as ex:
>E_lines = []
>E_pairs = []
>M = None
>info = "Error: " + str(ex)

滚边法

import math
from operator import itemgetter
import Rhino.Geometry as rg

def dist_xy(a, b):
    return math.hypot(a.X - b.X, a.Y - b.Y)

def start_index_minY_maxX(pts):
    # Y 最小，若相同 X 最大
    imin = None
    best = (float('inf'), -float('inf'))  # (Y升序, X降序)
    for i, p in enumerate(pts):
        key = (p.Y, p.X)
        if key[0] < best[0] or (abs(key[0]-best[0]) < 1e-15 and key[1] > best[1]):
            best = key
            imin = i
    return imin

def build_neighbors(pts, R, tol=1e-6):
    n = len(pts)
    adjs = [[] for _ in range(n)]
    thr = max(R, 0.0) + tol
    for i in range(n):
        pi = pts[i]
        for j in range(i+1, n):
            pj = pts[j]
            d = dist_xy(pi, pj)
            if d <= thr and d > tol:  # 排除重合点
                adjs[i].append(j)
                adjs[j].append(i)
    return adjs

def angle_key(origin, direction, pt):
    vx = pt.X - origin.X
    vy = pt.Y - origin.Y
    dx, dy = direction
    dot = dx * vx + dy * vy
    crs = dx * vy - dy * vx
    ang = math.atan2(crs, dot)
    if ang < 0: ang += 2 * math.pi
    return ang

def sort_neighbors_by_polar(pts, neighbors, current_idx, prev_idx):
    origin = pts[current_idx]
    if prev_idx is None:
        direction = (1.0, 0.0)  # 初始基准向量 (1,0)
    else:
        pv = pts[prev_idx]
        direction = (pv.X - origin.X, pv.Y - origin.Y)
        if abs(direction[0]) < 1e-15 and abs(direction[1]) < 1e-15:
            direction = (1.0, 0.0)
    neighbors.sort(key=lambda j: angle_key(origin, direction, pts[j]))

def circle_center_right(a, b, r, tol=1e-12):
    # 以 a,b 为弦，半径 r 的圆的“右侧”圆心
    dx = b.X - a.X
    dy = b.Y - a.Y
    d2 = dx*dx + dy*dy
    if d2 < tol:
        return None  # 重合
    # 若弦长大于 2r，无法构造圆
    if d2 > (2.0*r + 1e-12)**2:
        return None
    cx = 0.5 * (a.X + b.X)
    cy = 0.5 * (a.Y + b.Y)
    val = (r*r) / d2 - 0.25
    if val < 0:
        return None
    s = math.sqrt(max(0.0, val))
    # 右侧中心（与示例中的 cx - dy*s, cy + dx*s 保持一致）
    return rg.Point2d(cx - dy * s, cy + dx * s)

def point_in_circle_xy(p, center, r, tol=1e-9):
    dx = p.X - center.X
    dy = p.Y - center.Y
    return (dx*dx + dy*dy) <= (r*r - tol)

def has_points_in_circle(pts, neighbor_ids, center, r, exclude_idx):
    # 仅检查同一 R 邻域内的点是否落入圆内
    for k in neighbor_ids:
        if k == exclude_idx:
            continue
        if point_in_circle_xy(pts[k], center, r):
            return True
    return False

def get_next_point_ball(prev_idx, cur_idx, pts, adjs, r, flags):
    # 在 cur 的 R 邻域 adjs[cur_idx] 内寻找下一点（滚球法）
    nbrs = list(adjs[cur_idx])
    if not nbrs:
        return -1
    sort_neighbors_by_polar(pts, nbrs, cur_idx, prev_idx)
    pc = pts[cur_idx]
    for j in nbrs:
        if flags[j]:
            continue
        pj = pts[j]
        ctr = circle_center_right(rg.Point2d(pc.X, pc.Y), rg.Point2d(pj.X, pj.Y), r)
        if ctr is None:
            continue
        if not has_points_in_circle(pts, nbrs, ctr, r, j):
            return j
    return -1

def suggest_R_by_second_neighbor(pts):
    # 建议的 R：最大“第二近邻距离”，保证每点至少 2 个 R 邻居
    n = len(pts)
    if n < 3:
        return 0.0
    max_second = 0.0
    for i in range(n):
        pi = pts[i]
        dists = []
        for j in range(n):
            if j == i:
                continue
            d = dist_xy(pi, pts[j])
            dists.append(d)
        dists.sort()
        if len(dists) >= 2:
            max_second = max(max_second, dists[1])
        elif len(dists) == 1:
            max_second = max(max_second, dists[0])
    return max_second


def concave_hull_ball(S, R, tol=1e-6):
    if not S or len(S) < 3:
        return [], None, {"error": "点数量不足(<3)"}

    # 按 XY 去重（可选：简单容差去重）
    pts = []
    seen = set()
    scale = 1.0 / max(tol, 1e-9)
    for p in S:
        key = (int(round(p.X * scale)), int(round(p.Y * scale)))
        if key in seen:
            continue
        seen.add(key)
        pts.append(rg.Point3d(p.X, p.Y, p.Z))

    n = len(pts)
    if n < 3:
        return pts, None, {"error": "去重后点数量不足(<3)"}

    # 若 R 无效，给出建议值
    R_in = float(R) if R is not None else 0.0
    if not (R_in > 0.0):
        R_in = suggest_R_by_second_neighbor(pts)

    r = 0.5 * R_in  # 滚球半径
    adjs = build_neighbors(pts, R_in, tol)

    # 选择起点 A：Y 最小，若相同 X 最大
    i0 = start_index_minY_maxX(pts)
    if i0 is None:
        return [], None, {"error": "未能选取起点"}

    # 主循环
    flags = [False] * n
    hull_indices = [i0]
    prev_idx = None
    cur_idx = i0

    # 首先寻找初始 B（长度 < R，且对应圆满足“空弦”条件）
    j = get_next_point_ball(prev_idx, cur_idx, pts, adjs, r, flags)
    if j == -1:
        # 邻域太小，无法起步
        Pts = [pts[i] for i in hull_indices]
        return Pts, None, {
            "note": "未找到初始弦；R 可能过小",
            "points": n,
            "used": len(hull_indices),
            "R_used": R_in
        }

    hull_indices.append(j)
    flags[j] = True
    prev_idx = cur_idx
    cur_idx = j

    # 继续滚球
    safety = 0
    safety_limit = 10 * n + 10
    while safety < safety_limit:
        safety += 1
        j = get_next_point_ball(prev_idx, cur_idx, pts, adjs, r, flags)
        if j == -1:
            break
        # 若再次命中已经在弦上的点，结束
        if j in hull_indices:
            # 尝试闭合
            if j == hull_indices[0]:
                hull_indices.append(j)
            break
        hull_indices.append(j)
        flags[j] = True
        prev_idx, cur_idx = cur_idx, j

    # 构造输出点序列
    Pts = [pts[i] for i in hull_indices]

    # 若未显式闭合，但“首末距离 <= R”且通过圆检查，则尝试闭合
    Crv = None
    if len(Pts) >= 3:
        close_needed = (dist_xy(Pts[0], Pts[-1]) > tol)
        can_try_close = (dist_xy(Pts[0], Pts[-1]) <= R_in + tol)
        if close_needed and can_try_close:
            # 用最后一条弦（prev_idx, cur_idx），尝试将首点作为下一点
            last_prev = hull_indices[-2] if len(hull_indices) >= 2 else None
            last_cur = hull_indices[-1]
            # 构造“闭合弦”的圆检查
            nbrs = list(adjs[last_cur])
            if hull_indices[0] in nbrs:
                ctr = circle_center_right(
                    rg.Point2d(Pts[last_cur].X, Pts[last_cur].Y),
                    rg.Point2d(Pts[0].X, Pts[0].Y),
                    r
                )
                if ctr is not None and not has_points_in_circle(pts, nbrs, ctr, r, hull_indices[0]):
                    Pts.append(Pts[0])

        # 构造 PolylineCurve
        try:
            Crv = rg.Polyline(Pts).ToPolylineCurve()
        except:
            Crv = None

    stats = {
        "points": n,
        "R_used": R_in,
        "ball_radius": r,
        "neighbors_ok": all(len(adjs[i]) >= 1 for i in range(n)),
        "hull_vertices": len(Pts)
    }
    return Pts, Crv, stats


if 'tol' not in globals() or tol is None:
    tol = 1e-6

try:
    Pts, Crv, st = concave_hull_ball(S, R, tol)
    # 友好信息
    if isinstance(st, dict):
        info = " | ".join(f"{k}: {v}" for k, v in st.items())
    else:
        info = str(st)
except Exception as ex:
    Pts = []
    Crv = None
    info = "Error: " + str(ex)